南京大学 软件分析 课程总结
课程网站,在线评测,课程视频,silverbullettt。
知难而进,贵在坚持。省察体悟,贵于改过。
Course Introduction
概念
程序设计语言(Programming Languages,PL),静态程序分析(Static Program Analysis),莱斯定理(Rice’s Theorem),可靠性(Soundness)和完备性(Completeness)。
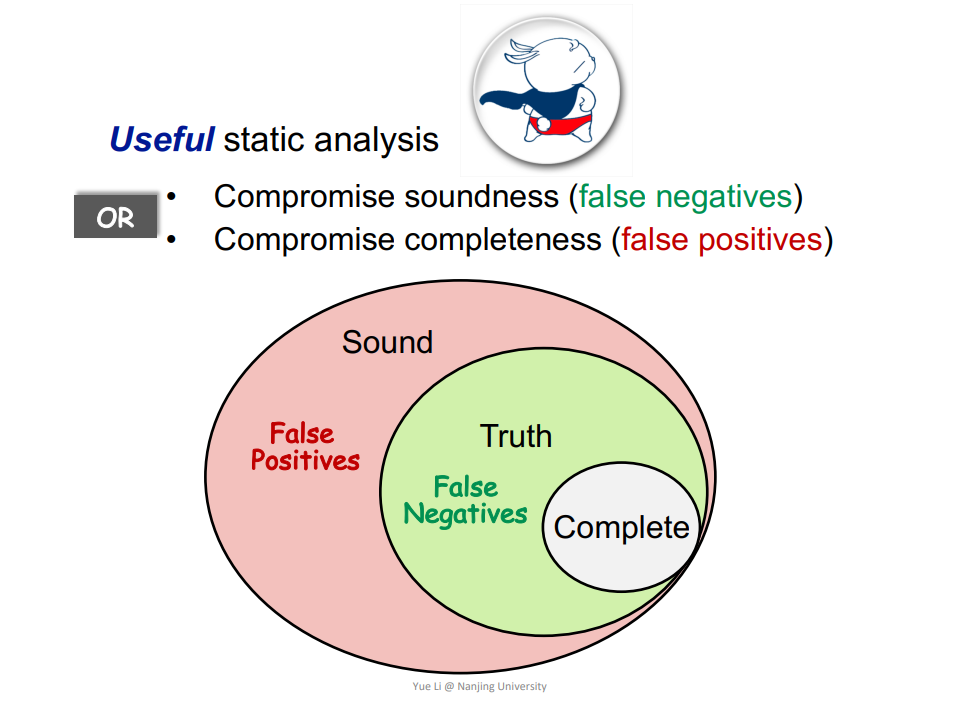
莱斯定理说明,不存在完美的静态分析,满足 Sound(Overapproximate)和 Complete(Underapproximate)。Sound 允许误报(false positives),但不允许漏报(false negatives),Complete 相反。
静态分析可以使用两个词概括:Abstraction + Safe-approximation(Transfer functions,Control flows)。首先对数据做抽象,然后对数据流做近似。近似涉及到 Transfer functions 如何设计和 Control flows 如何合并。Safe-approximation 的含义取决于使用场景,在大多数场景 Sound 就是 Safe-approximation,而小部分场景 Complete 才是。
问题
Q:关于静态分析,思考 What、Why、How?
Q:如何使用一句话概括静态分析?什么是有用的静态分析?
A:在确保 Safe-approximation 的前提下,在精度(precision)和速度(speed)之间权衡。
参考
Intermediate Representation
概念
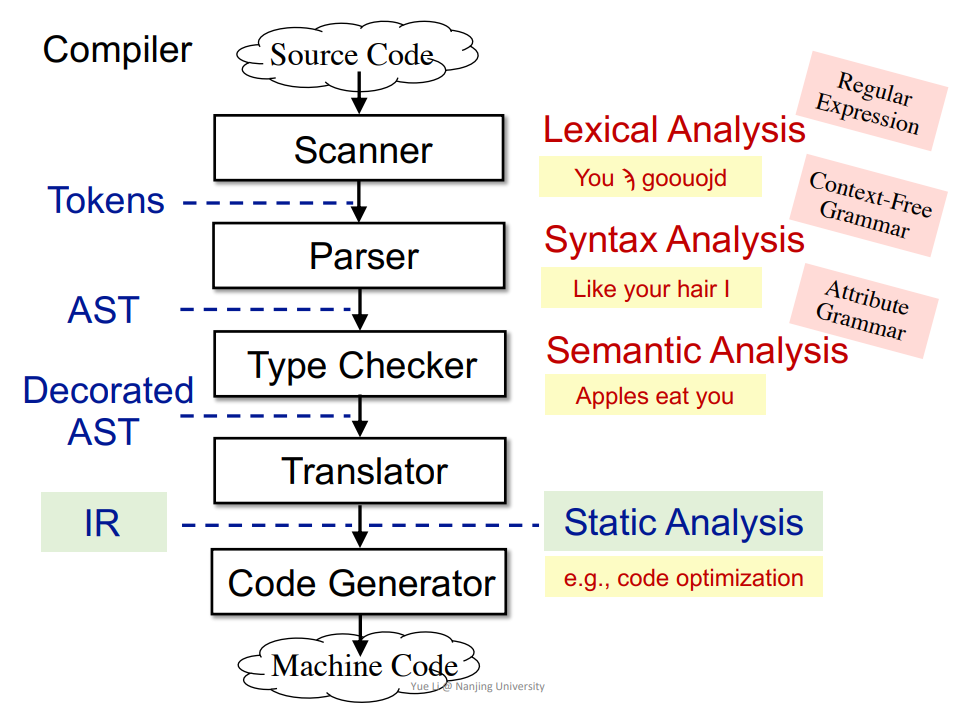
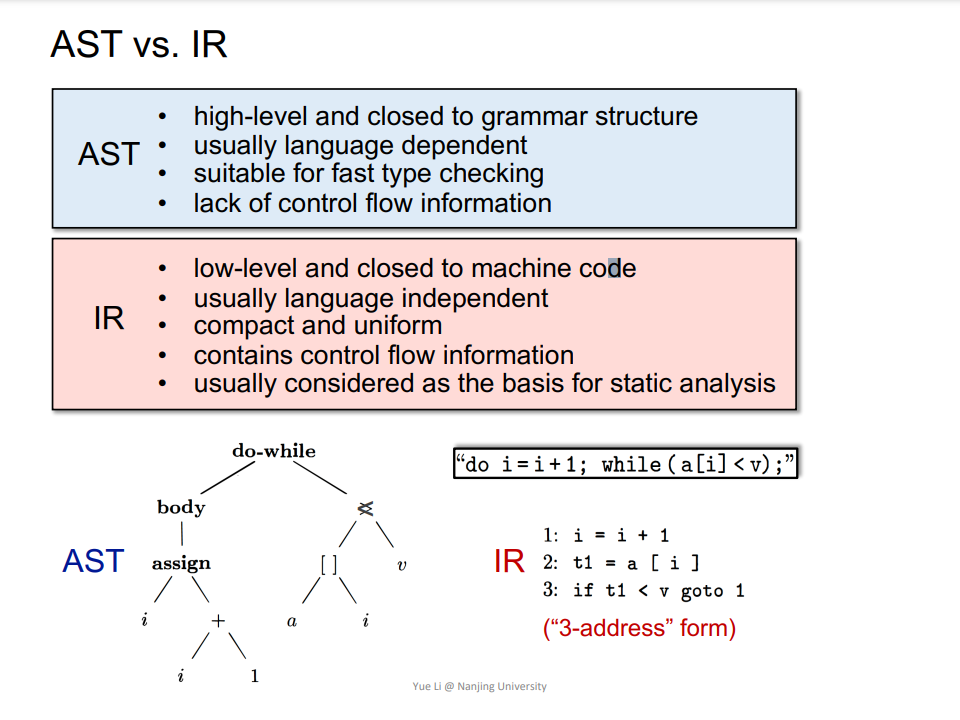
编译器(Compiler),中间表示(Intermediate Representation,IR),三地址码(Three-Address Code,3AC),控制流图(Control Flow Graph,CFG),基本块(Basic Block,BB)。
问题
Q:如何基于 3AC 构建 BB?如何基于 BB 构建 CFG?
参考
Data Flow Analysis - Applications
概念
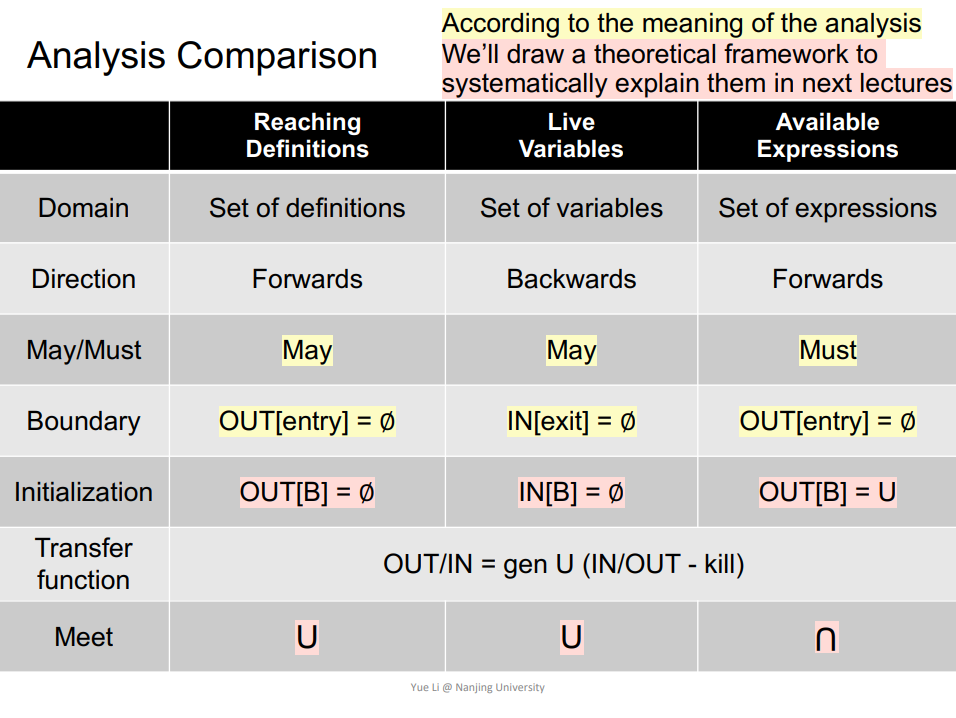
数据流分析的种类:may analysis(over-approximation),must analysis(under-approximation)。
数据流分析的应用:Reaching Definitions Analysis,Live Variables Analysis,Available Expressions Analysis。
问题
Q:为什么 Reaching Definitions Analysis 的算法最终会停止?
A:所有的 OUT 对应的 Bit Vector,它包含的 1 的数量都是单调递增的,最后必定会到达一个上界。
Q:为什么 Live Variables Analysis 使用 Backward Analysis,而不是 Forward Analysis?(算法设计更方便)
参考
Data Flow Analysis - Foundations
概念
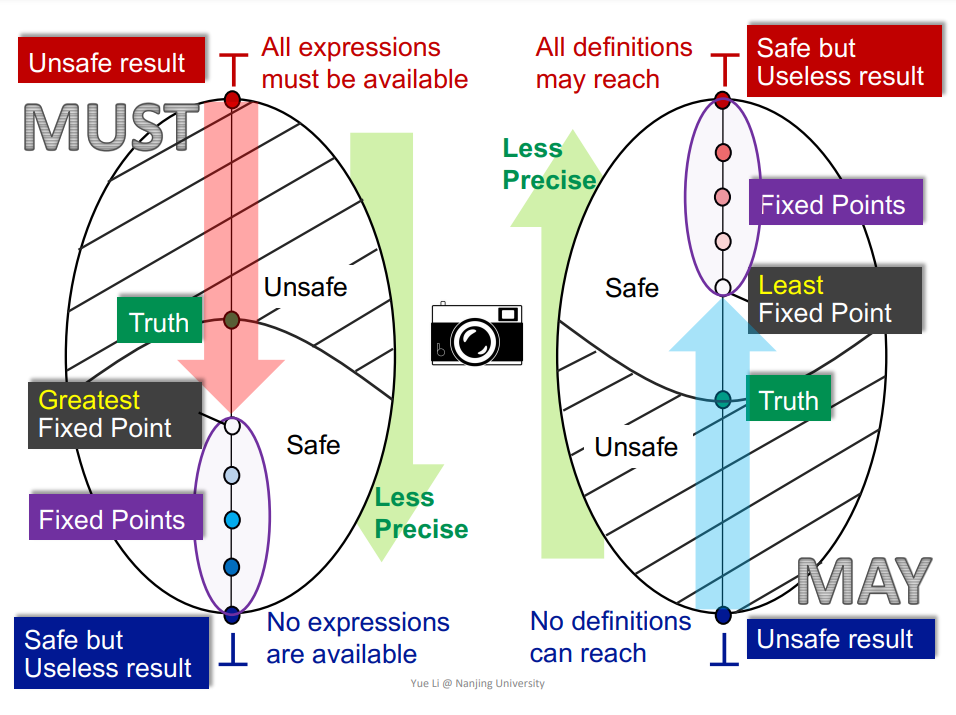
不动点(Fixed point),偏序集(Partially ordered set),上确界和下确界(LUB and GLB,Join and meet),格(Lattice),不动点定理(Knaster–Tarski theorem),抽象解释(Abstract interpretation)。
| Data Flow Analysis | Domain | Direction | May/Must |
|---|---|---|---|
| Constant Propagation Analysis | Set of pairs (variable, value) | Forwards | Must |
问题
Q:什么是 Meet-Over-All-Paths Solution(MOP)?MOP 和 Iterative Algorithm 的精度有什么关系?
Q:为什么 Constant Propagation Analysis 的 Transfer function 是不可分配的(Non-distributivity)?
Q:如何理解可能存在多个不动点,以及 Iterative Algorithm 求到的是最小/最大不动点?为什么在 Constant Propagation Analysis 中,MOP 的精度大于 Iterative Algorithm 的精度?MOP 是否满足不动点定理?
A:对于函数 \(F\) 而言,可能有多个 \(x\) 使得 \(F(x)=x\),所以可能存在多个不动点。由于 Iterative Algorithm 满足不动点定理,对于特定的函数 \(F\),如果存在多个不动点,我们求到的必然是最小/最大不动点。MOP 和 Iterative Algorithm 的函数 \(F\) 不同,所以 MOP 的精度可以更大,不会违背不动点定理。MOP 应该是满足不动点定理的,因为 Transfer function 和 Join/Meet function 相比 Iterative Algorithm 没有变化,只是它们组成的函数 \(F\) 有变化。
参考

Interprocedural Analysis
问题
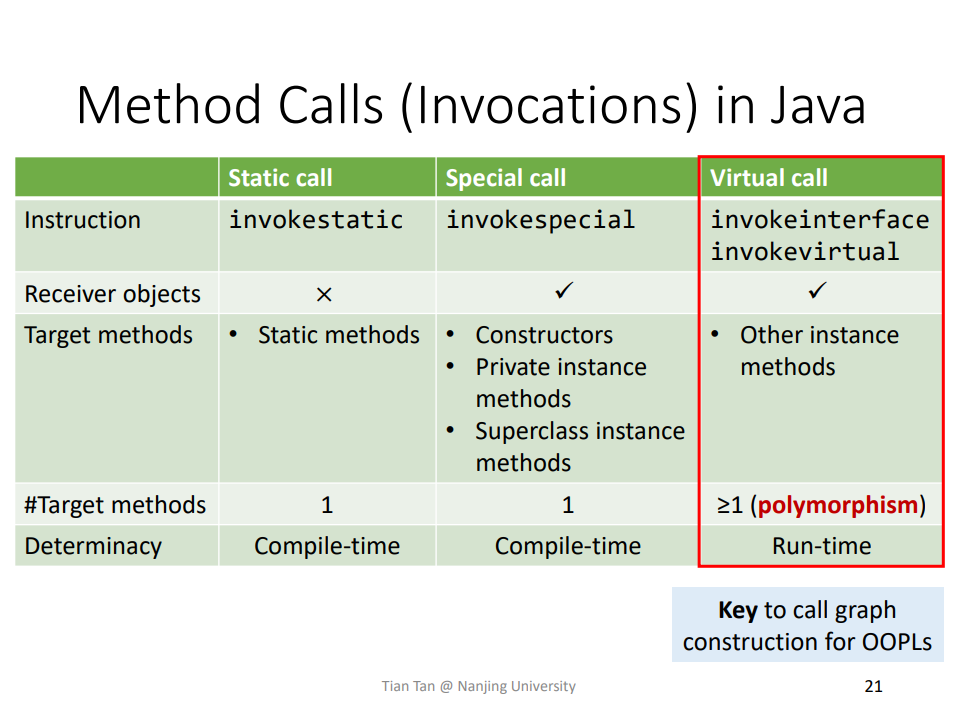
Q:什么是 CHA?如何基于 CHA 构建 Call Graph?
Q:如何实现 Interprocedural Constant Propagation Analysis?
参考



Pointer Analysis
问题
Q:Pointer Analysis 和 Alias Analysis 的区别?
A:Pointer Analysis 回答一个指针能指向哪些对象,Alias Analysis 回答两个指针是否能指向同一个对象。
Q:各个 Factor 的方案该如何选择,精度和速度的权衡?
A:课程选择 Allocation-site,Context-sensitive,Flow-insensitive,Whole-program。
参考



Pointer Analysis - Foundations
问题
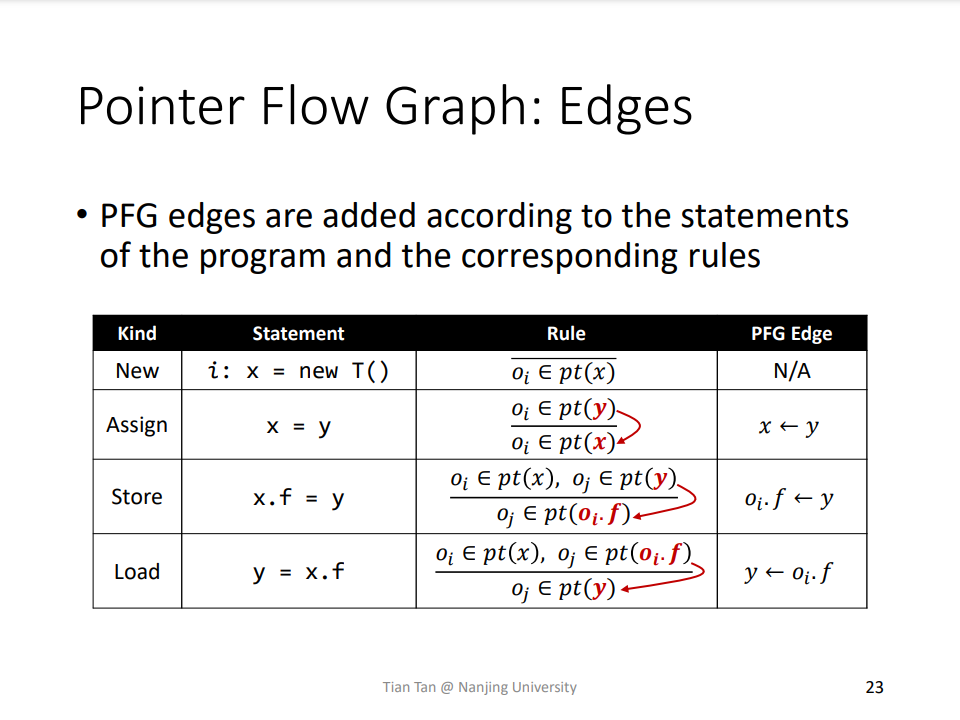
Q:什么是 Pointer Flow Graph(PFG)?如何构建 PFG?
Q:为什么构建 PFG 和在 PFG 上传播指向信息,两个过程相互依赖?以及构建 PFG 和构建 Call Graph 相互依赖?
A:首先需要有 PFG,才能在 PFG 上传播指向信息。而 PFG 节点获得指向信息之后,可能会在 PFG 中添加边。主要原因是 PFG 使用抽象对象的字段 \(o_{i}.f\) 来表示实例字段 \(x.f\),其中 \(o_{i}\in pt(x)\),它是动态变化的。为什么不直接使用 \(x.f\) 作为节点,在最开始将所有边建好?个人理解,如果 \(x\) 和 \(y\) 的指向信息存在交集,当更新 \(x.f\) 时需要部分更新 \(y.f\),这样很难使用图上的算法来实现 Pointer Analysis,所以需要做更细粒度的划分。构建 PFG 和构建 Call Graph 相互依赖,也是取决于 Call Rule 的设计,从而在构建 Call Graph 的过程中会在 PFG 中添加边。
参考





Pointer Analysis - Context Sensitivity
问题
Q:为什么 Instance fields 不需要限定上下文?
A:明确限定上下文的作用是什么,区分对同一个方法的多次调用,也就是区分多次调用中的变量和对象。而对于 Instance fileds 不需要区分什么,它从属于某个对象,该对象已经被上下文限定。
参考




Static Analysis for Security
参考





实验作业

如何减少和检查代码的错误?
① 编写代码前:可以先使用注释梳理逻辑,确定算法步骤。重要!如果遗漏某种情况,之后找错会花费更多时间。遇到不清楚的地方要及时(使用 TODO)标出来,不要想当然。② 编写代码时:不要过早优化。在必要的地方添加断言。当找不到想要的 API 时可以查看继承关系,目标 API 可能在子类中。每完成一个功能,就编写相应的测试用例,尽早发现问题。③ 代码出错时:首先检查逻辑是否有误/遗漏,以及边界条件的处理是否有误/遗漏。然后检查 API 是否存在误用,例如对 API 的功能理解有误,或者误用其他类的相同名称的 API。最后检查文档表述是否存在歧义,或者不清楚的地方,从而在实现细节的理解上存在偏差。④ 找不到错时:如果可以的话,找到正确代码,然后对拍测试。休息一下,或许之后能找到。真的找不到,重写一遍,或许能够发现遗漏的地方。真的真的找不到,寄。
Java 的 ArrayDeque 不能存储 null,而 LinkedList 可以。Deque 的文档有说明:
While
Dequeimplementations are not strictly required to prohibit the insertion of null elements, they are strongly encouraged to do so. Users of anyDequeimplementations that do allow null elements are strongly encouraged not to take advantage of the ability to insert nulls. This is so becausenullis used as a special return value by various methods to indicate that the deque is empty.
南京大学 软件分析 课程总结